Contents
FAQ
What are metaheuristics?
Metaheuristics are a class of optimization algorithms often inspired by natural processes, genetic algorithm being the prime example. Their main advantage is generality. Metaheuristics can be applied when no specialized algorithms for the problem exist or the exact algorithms are prohibitively slow.
What are the project goals?
- Developing new optimization algorithms and increasing the efficiency of the existing ones.
- Creating a software framework that incorporates various metaheuristics and allows to easily experiment and apply them to different problems.
What are the applications?
In principle, metaheuristics are applicable to any problem for which the quantity that needs to be optimized can be computed efficiently. These include both applied and purely mathematical ones. Travelling salesman problem is a classic example: find the shortest closed tour that visits each city from a given list exactly once. Several best-known solutions to difficult mathematical problems have been obtained with the aid of the framework.
Introduction
The goal of global optimization is the search of a solution that maximizes or minimizes an objective function defined over a search space of all possible solutions. Project Ascension is a research programme aimed at the development of a general-purpose global optimization framework. Its core components are intelligent algorithms called metaheuristics, which are applicable to a wide variety of optimization problems. Metaheuristics are often inspired by biological or physical processes: genetic algorithm mimics evolution, simulated annealing imitates a technique in metallurgy, etc. Due to the ability to explore very large search spaces, they can solve problems often intractable by other methods, for example those from the NP-hard class. Unlike the exact search methods like backtracking or branch and bound, they do not guarantee truly optimal results, but can arrive at high quality solutions in reasonable time. Generality of metaheuristics stems from their making very few assumptions about the search space, treating the problem in a black box manner. For example, unlike the classic local optimization methods, no derivatives are required for continuous problems.
The goals of the present project are:
- A theoretical and experimental study of metaheuristics to gain a better understanding of their behaviour.
- Software implementation of various metaheuristics suitable for both experimentation and practical problem solving.
While the software framework has reached a stage of maturity, the project is still far from being complete. An extensive experimental study of different metaheuristics across a broad range of problems is planned as the next step.
Algorithms
Ascension supports many metaheuristics, some well known and some original. Here is an incomplete list of presently implemented classes of algorithms:
Local search (LS) iteratively selects an improved solution from the current solution's neighbourhood. If an improvement can no longer be found, the search terminates and the last obtained solution is called locally optimal. LS can be quite fast, since only a small fraction of the search space is investigated at each iteration. Time complexity is usually polynomial in problem size. Its main disadvantage is the inability to explore more than one local optimum, which may be significantly worse than a global optimum. A number of important LS modifications is included. Variable neighbourhood search expands neighbourhood size upon failure to find an improvement. Tabu search maintains a list of already visited states and forbids returning to them, giving the algorithm exploration ability. Iterated local search perturbs a solution to avoid being trapped in a single local optimum. A novel modification called Chained Local Search performs multiple moves during one iteration, which results in greater efficiency.
Simulated Annealing (SA) mimics the annealing process in metallurgy, which relieves the internal stress of a material by heating it up and then slowly cooling it back down. SA overcomes the tendency of LS to get stuck by allowing occasional moves to worse solutions. Allowed degree of deterioration is determined by a parameter called temperature. At high temperatures, all moves are accepted (random search), and at low temperatures only improving moves are accepted (local search). SA gradually changes temperature from high to low using a cooling schedule. The exact form of this schedule has a major impact on optimization efficiency and is a subject of the current research. Thermodynamic notion of heat capacity proves very useful in this context. Based on empiric models of heat capacity, explicit analytical forms of new highly efficient cooling schedules have been obtained. Hybrid population-based modifications of SA are supported as well.
Genetic Algorithm (GA) is inspired by the process of biological evolution. The algorithm maintains a population of solutions subject to evolutionary processes. Offspring solutions are created by crossover of parent solutions and random mutations and replace less fit solutions within the population. Replacement and parent selection methods ensure that high quality solutions reproduce and survive. A very important issue with the GA is the maintenance of biological diversity. The use of simple selection and replacement methods that favour better solutions without regard to diversity leads to a rapid proliferation of few genetic traits. This usually results in a loss of diversity and premature convergence to solutions of poor quality. Various techniques of countering the problem are implemented.
Distribution Algorithms maintain an explicit model rather than a population of solutions. In the Estimation of Distribution Algorithm (EDA), new solutions are sampled from this model. The better samples are then used to update the existing model or to create a new one. A positive feedback loop thus drives the model towards better regions of the search space. Ant Colony Optimization (ACO) is based on ants' foraging behaviour. As ants search for food, they lay down trails of chemicals known as pheromones. These trails gradually evaporate, so routes that take less time to travel end up having higher pheromone concentration and attract other ants. This way a colony quickly locates the shortest path to the food source. In ACO, ants correspond to solutions and pheromone concentrations correspond to the distribution model. While EDA and ACO have been developed independently, they are very similar from the algorithmic viewpoint. A generalized algorithm that incorporates both EDA and ACO is provided.
Swarm Intelligence algorithms take inspiration from the behaviour of collective animals. Insect swarms, bird flocks and schools of fish are a few examples. Interaction of individuals within the swarm gives rise to complex emergent behaviour. The best known algorithm from this class is the Particle Swarm Optimization, which is limited mostly to continuous problems. A novel swarm intelligence algorithm suitable for both continuous and discrete problems is offered.
Problems
Ascension framework has a modular structure, with algorithms and problem description being located in separate loosely coupled modules. Such an orthogonal design results in great flexibility. Problem-specific data types, operations and the objective function are contained in a problem definition module (PDM). Adapting to a new problem is fairly easy and only requires writing a new PDM, while all the optimization algorithms are left intact. The ability to quickly switch between problems is very useful, as it allows to investigate the behaviour of different metaheuristics in a problem-independent manner. This uniform approach makes difference between genetic programming and other types of problems insignificant from the algorithmic viewpoint. Ascension is written in a compiled language (Delphi, a dialect of Pascal), and so are the PDMs. Combined with optimized code, this makes for a highly efficient system.
Here is an incomplete list of implemented problems:
- Travelling salesman problem: find the shortest closed tour that visits predefined points,
- N Queens: Place N queens on an N⨯N board so that no queen is attacked by another,
- Magic square design: fill an N⨯N array with numbers {1..N2} so that the sum of numbers in each row, column and diagonal is the same,
- Lennard-Jones clusters: minimize energy of a molecular configuration with pairwise potential U(r) = ε((r0 / r)12 - 2 (r0 / r)6)
- 2D HP protein folding model: minimize conformational energy of a sequence of aminoacids confined to two-dimensional square grid,
- Classic cryptanalysis: find the permutation of characters that decrypts a simple substitution cryptogram,
- Graph colouring: colour all vertices of a graph with a minimal number of colours so that no two vertices of the same colour are connected by an edge,
- Minimal linear arrangement: assign numbers {1..N} to N vertices of a graph so as to minimize the sum of absolute differences of numbers in adjacent vertices,
- Space-filling curves: find a curve with the highest locality that traverses an N⨯N square grid,
- Heilbronn problem: maximize the area of the smallest triangle formed by N points inside of a unit square,
- Sorting worst case analysis: find the numeric array of a given length whereupon a particular sorting algorithm performs the worst,
- Maximum density still life: find an N⨯N array with the highest number of live cells that is stable under the rules of the Game of Life cellular automaton,
- Neural network training: optimize synaptic weights of an artificial neural network,
- Metaheuristic programming: automatic discovery of programs, a generalized version of genetic programming.
Notable results
Interesting mathematical results obtained with the aid of the framework include:
- Best-known solutions to the Heilbronn problem
- Bounds for the maximal density axial subsquare-free arrangement problem
- Bounds for the peaceable queens problem
- Short Brainfuck programs
- Record-breaking chess positions
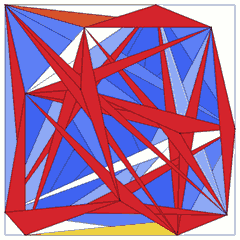
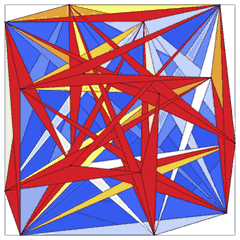
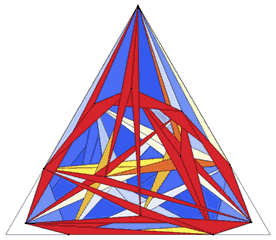
Some Heilbronn problem solutions for the unit square and triangular regions:
Source code
The latest version of Ascension can be found on Github. Please note that many features had to be omitted from the 2.0 release, but will be reimplemented in the future.