Contents
Multidimensional Scaling
Multidimensional Scaling (MDS) is a problem of finding a set of points whose pairwise distances match a given matrix as closely as possible. Simple iterative algorithm has been developed to find the MDS solutions. Compared to the well known SMACOF[1] algorithm, the new method has the advantages of avoiding poor quality local optima and being compatible with arbitrary loss functions.
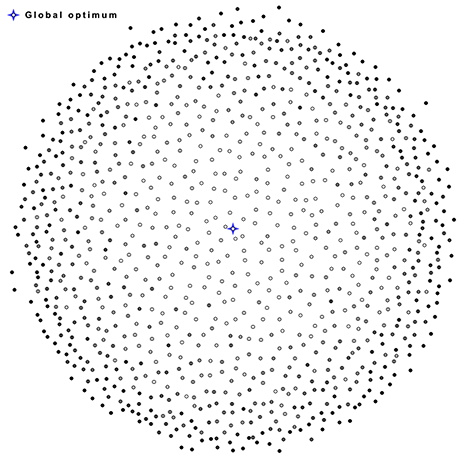
MDS is a powerful tool for data visualization. For example, it can be used to obtain a clear illustration of the travelling salesman problem solution space structure, confirming results of Boese[2].
MDS of 2-opt TSP tours for the PCB442 problem. Lighter points correspond to shorter tours.
Other interesting images generated by MDS can be found in the gallery.
Project status: Research: incomplete | Implementation: prototype | Tech report: none
Text Distance Metrics
Various metrics for measuring distance between two texts have been implemented. Ideally, the metrics could allow to quantitatively measure the differences in writing style between different authors. MDS technique described above can be applied to the text distances to build "literature maps".
MDS based on distances between novels by four different authors. Good clustering is observed despite the fact that Russian translations were used. T1 and T2 denote two different translations.
Project status: Research: incomplete | Implementation: prototype | Tech report: none
Image Upscaling
Traditional bilinear and bicubic interpolation methods can result in low quality enlarged images. They behave poorly around sharp object edges, introducing blurriness and ringing. Original upscaling method has been developed to avoid this problem.
Source image and x8 times upscales of the highlighted part using bicubic interpolation and the original method. Click to see full size images.
Project status: Research: incomplete | Implementation: prototype | Tech report: none
Digital Filtering
Original digital filters were designed to achieve good time domain accuracy. They are well suited for smoothing and computing derivatives of noisy data. Compared to the Savitzky-Golay filters, they are faster and easier to implement. Comparison of filtered signal quality is yet to be performed.
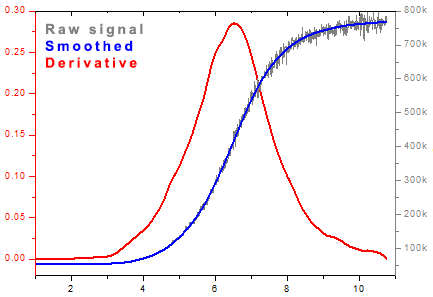
Project status: Research: incomplete | Implementation: complete | Tech report: none
Adaptive Smoothing
Exponential smoothing is a popular time series smoothing technique. Observation weights decrease exponentially: w(i) ~ Exp(-i / τ), where τ is a parameter controlling the smoothing strength. Double exponential smoothing also estimates a signal's derivative and is better suited for signals with linear trend. Quality of the smoothed signal depends on the choice of the parameter τ. Proper choice of τ may be impossible if no prior knowledge about the input data is available. A family of exponential smoothing methods with automatic parameter adaptation has been developed to deal with the problem. Optimality in terms of the filtered signal accuracy is proven for some members of the family under the assumption of white noise. The methods are completely parameter-free and compatible with both single and double exponential smoothing.
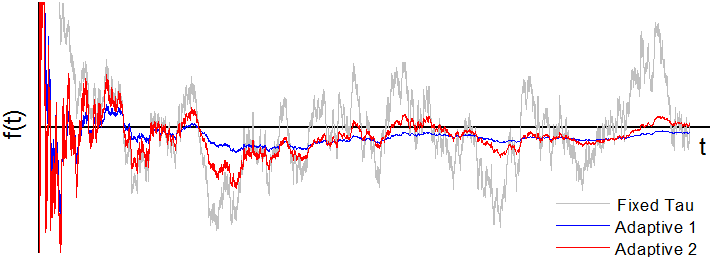
Comparison of single exponential smoothing with optimal fixed τ parameter and two adaptive methods. Input signal is a Gaussian white noise.
Project status: Research: incomplete | Implementation: complete | Tech report: incomplete
References
- De Leeuw J, Mair P. Multidimensional Scaling Using Majorization: SMACOF in R.
- Boese K D. Cost Versus Distance In the Travelling Salesman Problem.
My research has never been officially supported. You can contribute to further research at my Patreon page. Top patrons:
- Brian Bucklew
- Anton Shepelev
- Adam Hill
- Tomoyuki Naito
- John Metcalf